Recently, AI agents have demonstrated very promising developments in automating the proving of mathematical theorems and verification of the correctness of code using tools such as Lean. Such tools combine code with specifications and certifications to ensure that it meets intended requirements, providing a very powerful safeguard for safety-critical applications. Artificial intelligence has been proven to enable the fundamental steps of solution development: coding, specification, and proof through large-scale language models. Although these advances are very promising, fully automating program verification remains difficult.
Traditionally, proving mathematical theorems has relied on tools like Lean that train models on datasets like Mathlib and use specific definitions and strategies to solve problems. However, these tools struggle to adapt to program verification, which requires completely different methods and approaches. While machine learning has improved the automation of systems like Coq and Isabelle, Lean has yet to make similar advances in program verification. Other tools such as Dafny and Verus and benchmarks such as miniF2F and CoqGym also provide alternatives. Still, the challenge of adapting mathematical theorem proving methods to the needs of program verification has not been fully addressed.
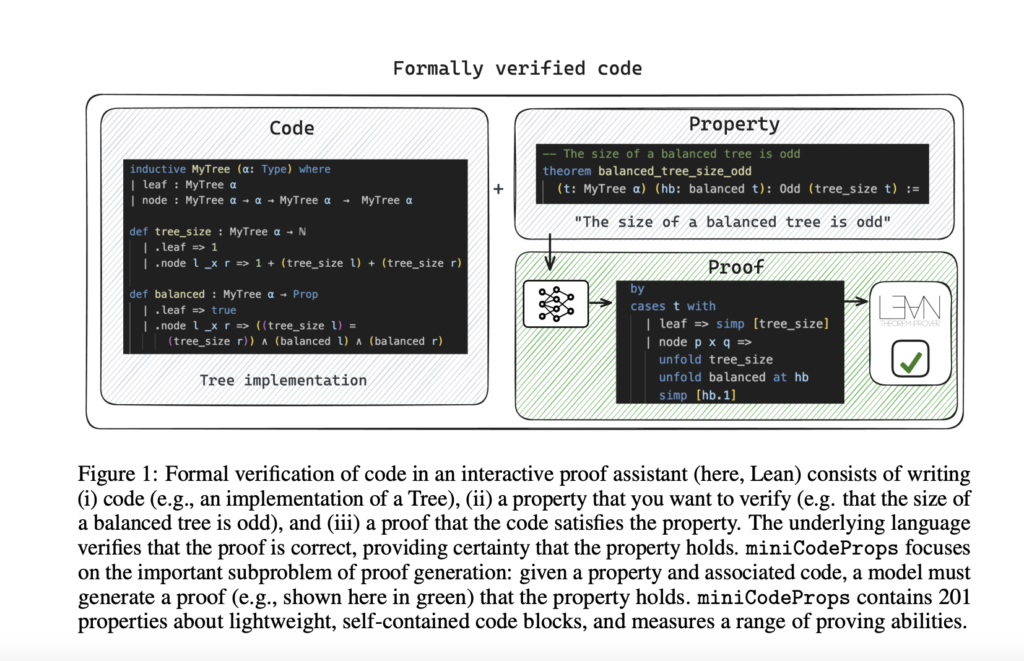
To solve this, researchers at Carnegie Mellon University applied miniCodeProps, a benchmark containing 201 program specifications to the Lean Proof Assistant, to address the challenge of automatically generating proofs for programs and their specifications. I suggested it. miniCodeProps contains simple self-contained programs such as lists, natural numbers, and binary trees of varying degrees of proof difficulty. This dataset is divided into three categories: intuitive properties of lists, trees, and numbers (Medley), termination lemmas for recursive functions (Termination), and properties of non-standard sorting algorithms (Sorting). Contains 201 theorem statements. The functions primarily operated on linked lists, and some included natural numbers and binary trees. These properties are categorized by difficulty: easy (medley), medium (finish), and difficult (sort). The termination lemma requires proving recursive termination, which was important for the use of Lean 4. The dataset, available in jsonlines format, includes important details such as the proof state and the dependencies of each theorem. Examples such as the zip over concatenation property and the sorting property highlighted the challenge of proving these properties, especially for more complex sorting algorithms.
The evaluation of miniCodeProps focused on two main tasks: complete proof generation and per-tactic generation. In generating a complete proof, the model was tested for its ability to generate a complete proof against a given specification. For tactic-by-tactic generation, models were evaluated based on their ability to suggest the next appropriate tactic from the current proof state, and incremental reasoning was tested. The evaluation also takes into account the difficulty of the proofs, from simple properties of lists and numbers to complex properties of termination and sorting algorithms, and measures both the efficiency and accuracy in generating proofs and applying tactics. Ta.
Results showed that neural theorem provers such as GPT-4o performed well on simple tasks, achieving a success rate of 75.6% on medley properties. However, performance on more difficult tasks such as termination and sorting was lower at 4.34% and 6.96%, respectively. The model ntp-ctx-1.3B, trained on Mathlib, demonstrated similar efficiency to GPT-4o, suggesting that domain-specific validation tools may be more promising. MiniCodeProps provides a framework to improve automated theorem proving agents for code verification, support human engineers, and provide additional guarantees through diverse inference approaches.
All in all, the proposed miniCodeProps is a valuable benchmark that can be used to advance automated ITP-based code verification. It contains problems from a variety of inductive problem datasets, allowing you to step through the properties of your program. However, this method has limitations and cannot effectively solve complex problems. MiniCodeProps potentially drives advancements in verification agents and serves as a baseline for evaluating new approaches in automated code verification.
Check out the paper. All credit for this study goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram channel and LinkedIn group. Don’t forget to join the 60,000+ ML SubReddit.
🚨 Trending: LG AI Research releases EXAONE 3.5: 3 open source bilingual frontier AI level models that deliver unparalleled command following and long context understanding for global leadership in exceptional generative AI….
Divyesh is a consulting intern at Marktechpost. He is pursuing a bachelor’s degree in agricultural and food engineering from the Indian Institute of Technology, Kharagpur. He is a data science and machine learning enthusiast who wants to integrate these cutting-edge technologies into the agricultural sector to solve challenges.
🧵🧵 (Download) Large-scale language model vulnerability assessment report (recommended)